Casa
scp 99999

🌗🐝 on X: 1/99999 interactions where they somewhat get along

Por um escritor misterioso

Descrição
🌗🐝 on X: 1/99999 interactions where they somewhat get along
I'm Settling This Math Debate Forever (.99 repeating = 1)
🌗🐝 on X: 1/99999 interactions where they somewhat get along
Algebra Unit 1 Challenge 2.docx - Sophia - College Algebra Unit 1 Challenge 2 Select the expression that is correctly evaluated. a. b. c. d. Use the
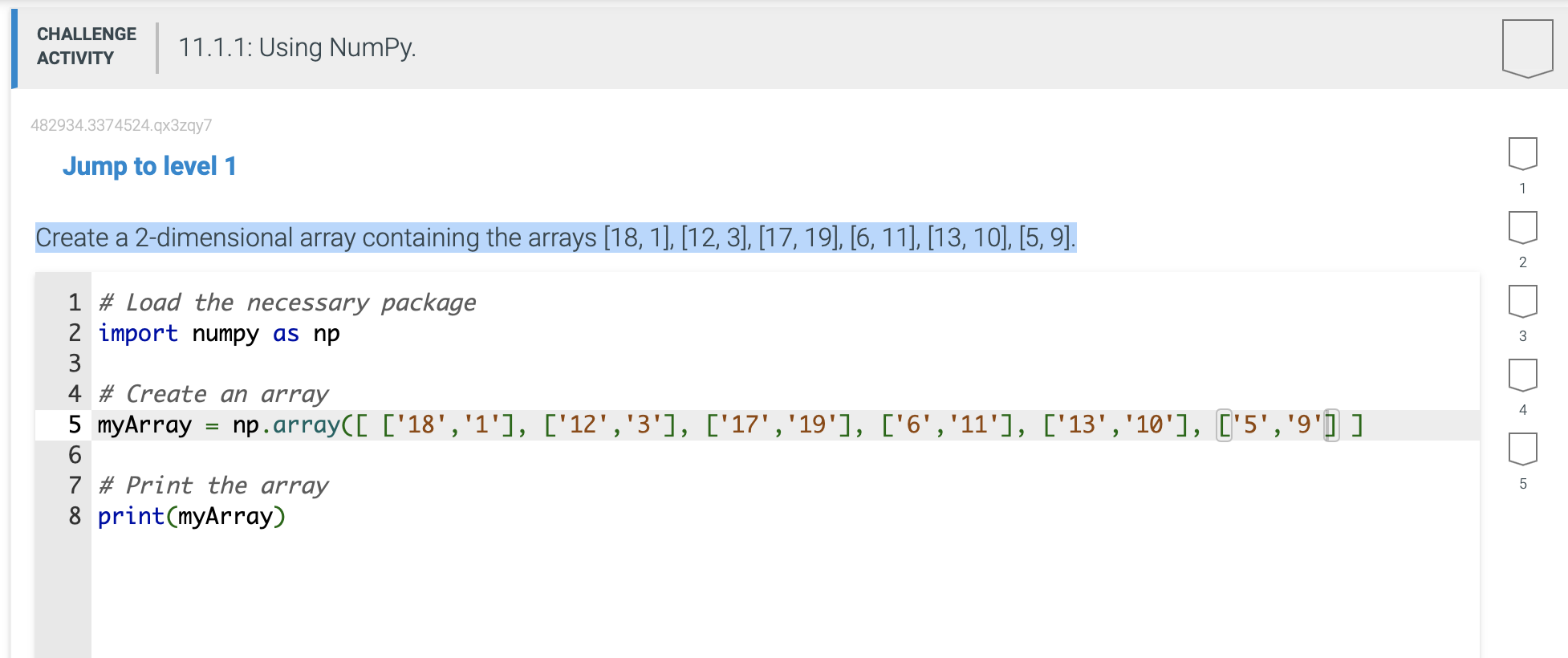
🌗🐝 on X: 1/99999 interactions where they somewhat get along
Solved CHALLENGE ACTIVITY 11.1.1: Using NumPy.
🌗🐝 on X: 1/99999 interactions where they somewhat get along
Problem Understanding Epsilon-Delta Handout - Mathematics Stack Exchange.pdf - Problem Understanding Epsilon-Delta Handout - Mathematics Stack Ex. 1 of
🌗🐝 on X: 1/99999 interactions where they somewhat get along
Solved I don't know where to start with this question. Can
🌗🐝 on X: 1/99999 interactions where they somewhat get along
🌗🐝 on X: 1/99999 interactions where they somewhat get along / X
🌗🐝 on X: 1/99999 interactions where they somewhat get along
Math 32 - WHW9 2 .pdf - Math 32 Written Homework #9 Fall 2022 Complete the following tasks. To show work for the double-integrals demonstrate that
🌗🐝 on X: 1/99999 interactions where they somewhat get along
Proof that .99999… is NOT equal to 1, by Kenneth Ahlstrom
🌗🐝 on X: 1/99999 interactions where they somewhat get along
Solved Could you show how to show exercise 3.31 with
🌗🐝 on X: 1/99999 interactions where they somewhat get along
Can't We All Just Get Along?
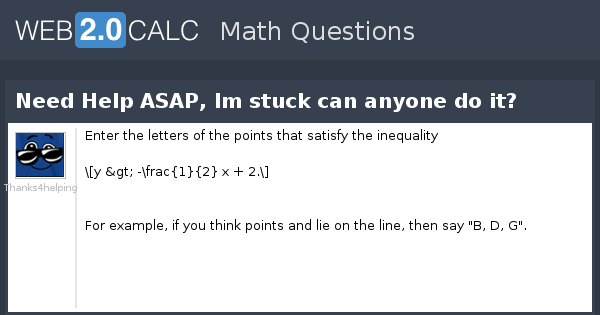
🌗🐝 on X: 1/99999 interactions where they somewhat get along
View question - Need Help ASAP, Im stuck can anyone do it?
🌗🐝 on X: 1/99999 interactions where they somewhat get along
Algebra Unit 1 Challenge 2.docx - Sophia - College Algebra Unit 1 Challenge 2 Select the expression that is correctly evaluated. a. b. c. d. Use the
🌗🐝 on X: 1/99999 interactions where they somewhat get along
I'm Settling This Math Debate Forever (.99 repeating = 1)
de por adulto (o preço varia de acordo com o tamanho do grupo)